Where Binary Heap is Used

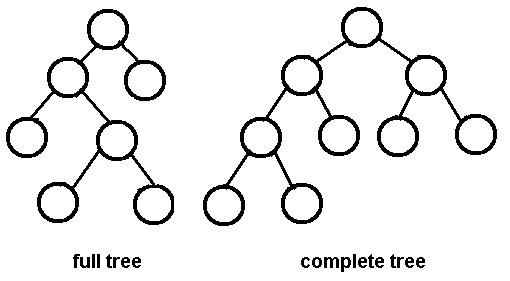
definitions

A full binary tree (sometimes referred to as a proper binary tree or plane binary tree) is a tree in which every node other than the leaves has two children. In other words, each node has either 0 child or 2 children. 

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

A perfect binary tree is a binary tree with all leaf nodes at the same depth. All internal nodes have degree 2.

Perfect Tree

A Binary Heap is a binary tree with following 2 properties:
​

1. A complete tree.
2. A Min Heap or Max Heap. In a Min Binary Heap, the key at root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree. Max Binary Heap is similar to Min Heap.

implementation

A very efficient way to implement a max heap is by using an array. To find an object’s children within the array we can use the formula:

leftChild = 2 * nodeIndex + 1
rightChild = 2 * nodeIndex + 2

To build a Heap it takes O(n):

def build_heap(A[1...n]):
 size <- n
 for i from n/2 downto 1:
  siftDown(i)

There are 4 major methods for implementing a max heap:

add()

When objects are first added to the heap they are initially added to the end of the heap (end of array). 

remove() 

Remove and return its largest object. The remove() method removes the root object (or first object in the array), immediately replaced with the last object in the heap, followed by siftDown()

siftUp()

The siftUp() method is used to move a newly inserted object from the last position in the array to its final location.

siftDown()
​
The siftDown() method is used to move the newly added root object (or first object in the array) to its correct position. 

applications

1. Heap Sort: Heap Sort uses Binary Heap to sort an array in O(nLogn) time.
2. Priority Queue: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time. 
3. Dijkstra’s Shortest Path: Min Heap to store the vertices not yet included in Shortest Path Tree (the unsettled set, or the vertices for which shortest distance is not finalized yet).  Min Heap is used as a priority queue to get the minimum distance vertex from set of not yet included vertices. Time complexity of operations like extract-min and decrease-key value is O(logn) for Min Heap.
4. Prim’s Minimum Spanning Tree
5. ​K’th Largest Element in an array (partial sorting)
6. Sort an almost sorted array
7. Merge K Sorted Arrays

comparison

Binary Heap vs. Binary Search Tree

By comparison, if a binary tree is sorted, items to the left of a particular node are smaller, items to the right are larger, then we call it Binary Search Tree. Binary Heap does not guarantees the order while Binary Search Tree does. A Balanced Binary Search Tree guarantees height of O(log n) for n items. 

Binary Heap vs. Red-Black Tree

Red-Black tree is a self-balancing binary search tree done by coloring each node in the tree with either red or black and preserving a set of properties that guarantee that the deepest path in the tree is not longer than twice the shortest one, while Binary Heap is a complete tree that guarantees the tree is balanced. 

references

• ​https://www.geeksforgeeks.org/applications-of-heap-data-structure/
• https://www.geeksforgeeks.org/binary-heap/​
• https://www.geeksforgeeks.org/greedy-algorithms-set-7-dijkstras-algorithm-for-adjacency-list-representation/
• http://bigdatums.net/2016/07/28/create-max-heap-using-an-array-java/
• https://towardsdatascience.com/course-2-data-structure-part-2-priority-queues-and-disjoint-set-ed11a0383011