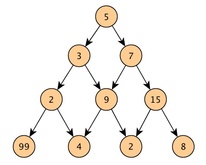
 Assuming we have a set of values (see left). If you write these values down on a a piece of paper, from the top element you can branch downward into either left or right element each has its value. You can get a set of values with triangular look as shown. The question is, going from the value at the top to the bottom by choosing to go down the path of either left or right, what is the maximum sum among all possible paths? The ApproachFirst choose a data structure (node, each point to left child or right child) to present the set of values, then use recursive to solve the problem. Thought ProcessAn intuitive way of solving this is to use node to represent the data structure, and use recursive approach to find the maximum sum among all paths. A node hold value as its data, has a left Node, and a right Node. An head/top Node can be initialized to represent the whole triangular set of values as seen in the main() below. The maximum sum among all paths starting from a given node is the max of its value plus either the maximum sum among all paths starting from either its left node or right node. Code Snippetimport java.util.*; The output of this program is 109. The PerformanceThe performance of the above recursive algorithm can be view as proportional to the number of various paths. Speaking of number of paths, should the level of the triangular set of numbers is 1, then the number of different paths is 1. If the level of the triangular set of numbers is 2, then the number of different paths is 2. If the level of the triangular set of numbers is 3, then the number of different paths is 4. In a nut shell, the number of different paths of a particular level doubles the previous level:
1 level -> 1 path 2 levels -> 2 paths 3 levels -> 4 paths 4 levels -> 8 paths 5 levels -> 16 paths Therefore, the big O notation of the above recursive algorithm is the number of paths which is 2^n where n is the number of level of the triangular set of values.
0 Comments
Leave a Reply. |
Categories
All
Archives
May 2020
|
 RSS Feed
RSS Feed