|
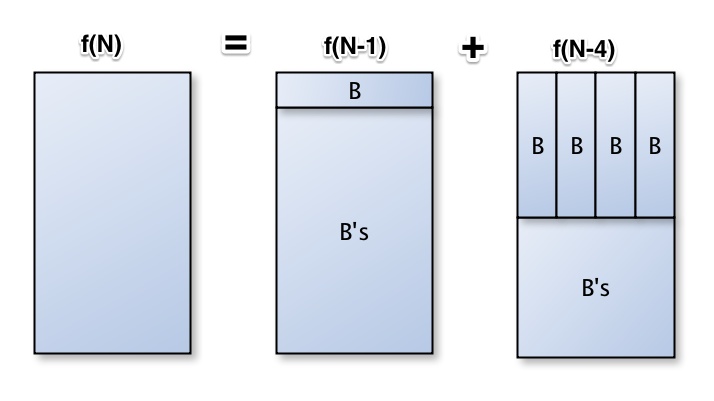
There is a wall of size 4xN. You have infinite supply of bricks of size 4x1 and 1x4 in the house. How many ways are there to fill out a wall of size 4xN? Thought ProcessThis can be addressed by dynamic programming. The characteristics of optimal substructure, recursive nature, and bottom-up approach were mentioned in this post. Let's say, number of ways to fill out a wall of size 4xN with infinite supply of 4x1 and 1x4 bricks is said to be f(N). Per common sense, we know: f(1) = 1 f(2) = 1 f(3) = 1 f(4) = 2 Also, when you think about it when filling out 4xN with f(N) ways of doing it, you can break f(N), when N >= 4, down to 2 substructures as below. Given the fact that one 4x1 can goes either horizontally or vertically. When it goes horizontally, there's only one way as shown in f(N-1). But when it goes vertically, all other 3 bricks may need to go vertically as well as seen in f(N-4) below. Code Samplepublic static int numberOfWays(int N){
1 Comment
Pushpender
10/1/2016 12:18:38 pm
Nice solution
Reply
Leave a Reply. |
Categories
All
Archives
May 2020
|
 RSS Feed
RSS Feed